Fractal Tree
| Angle | |
| Depth | |
| Asymmetry | |
| Length Decay |
A fractal is a geometric figure which displays self-symmetry, where splitting the figure into smaller parts, each of which will approximate the whole figure
The fractal tree is on of the simplest fractal figures, where at each node we generate two nodes, which are separated by an angle two ?.
This can be controlled by the parameter angle
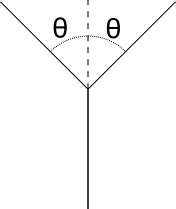
The process is recursive, until we reach a set leaf node. Here the recursion depth can be controlled through the parameter depth. The length between the old node and the new node decays with recursion depth, this decay can be controlled through the parameter length decay
The final parameter asymmetry controls the angle phi, this parameter controls offsets the angle theta, thus introducing an asymmetry to the figure
There are some extra finishing touches that have been applied to the figure, firstly the width of each branch is controlled by the recursion depth The lower the current recursion depth the wider the branch, this adds an extra aesthetic to the figure, making it look more tree like. The second is the grow feature, this rebuilds the tree in a timed sequence. Each timed step rebuilds the tree, with increasing recursion depth until the maximum depth has been reached. As the width of the branch is defined by the total recursion depth, as each figure is processed the tree appears to grow, not just in branches but also in width.