Calculating π with random numbers
The technique is called Monte Carlo integration, this technique allows us to perform numerical integration using random numbers. While not being an efficient method of calculating π it’s still an interesting method and a good introduction to the Monte Carlo method of integration.
The technique applies a random distribution of points within a system of known area A, the system contains a domain of unknown area B. The relative size of areas A and B can be estimated through the number of points that fall within the total system and the smaller domain. As the area of A is know, area B can be directly estimated using this ratio.
To estimate π, we require a system where the ratio between two domains is proportional to π. We can achieve this by using a square system with a circular domain, where the radius of the circle is half the width of the square.
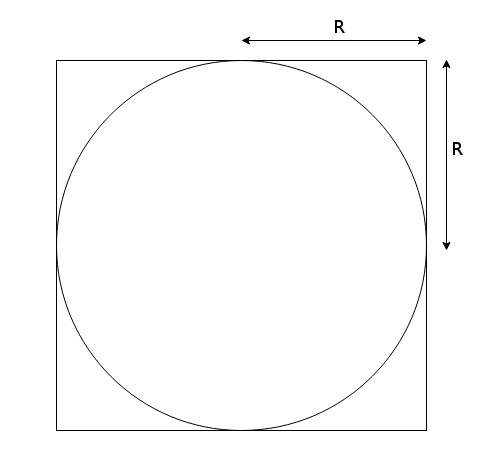
The area of the circle and square are known to be,
and
As both r terms are equal, we can join the two equations by this common term,
And rearranged for π,
Thus, we have shown that the ratio between the circular domain and the square domain is proportional to π. Now, applying random points to this system, we can approximate . Shown below is a random distribution of points for this system, with the points within the circular domain shown in blue, for increasing powers of ten.
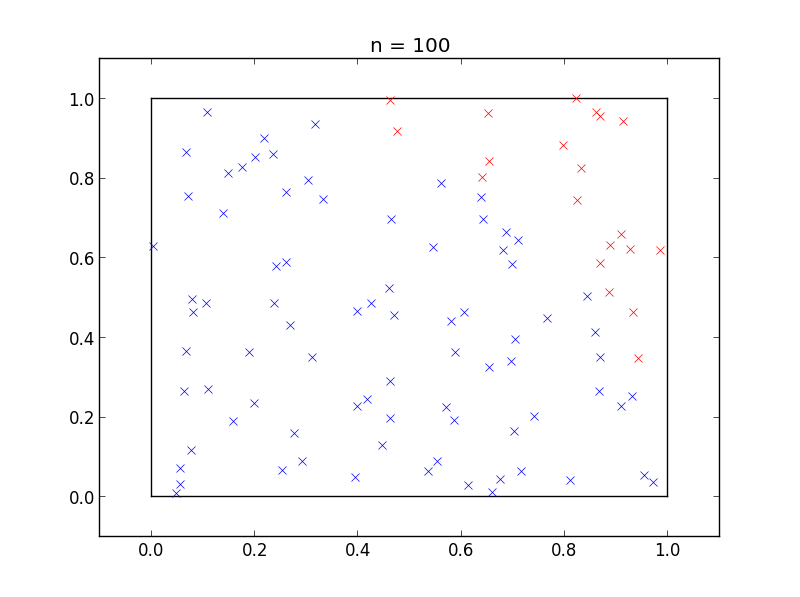
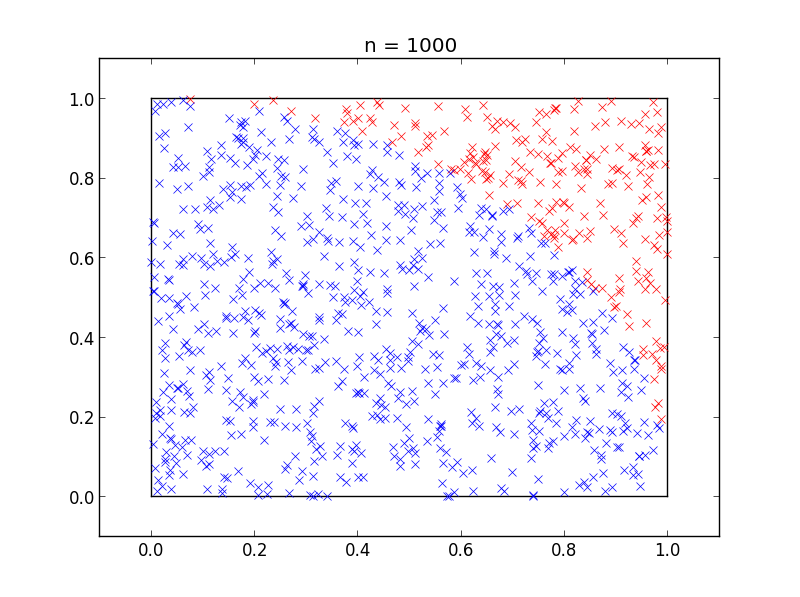
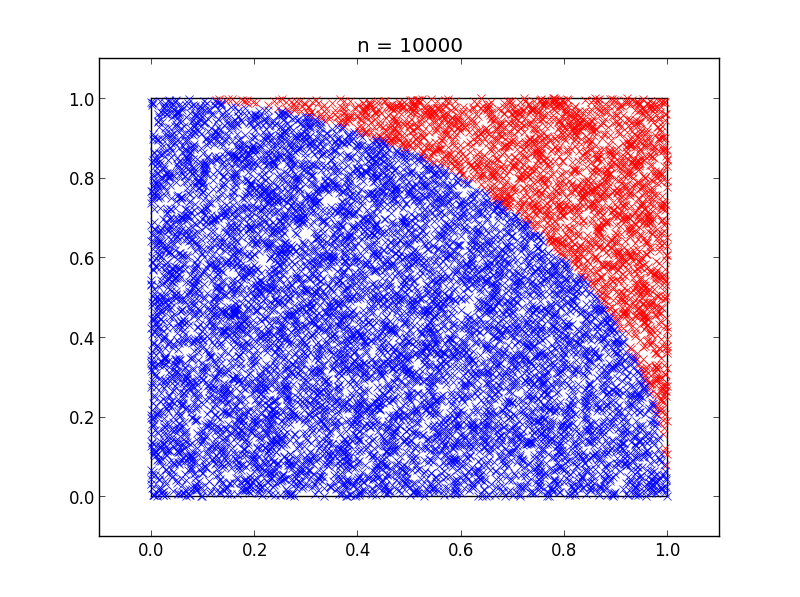
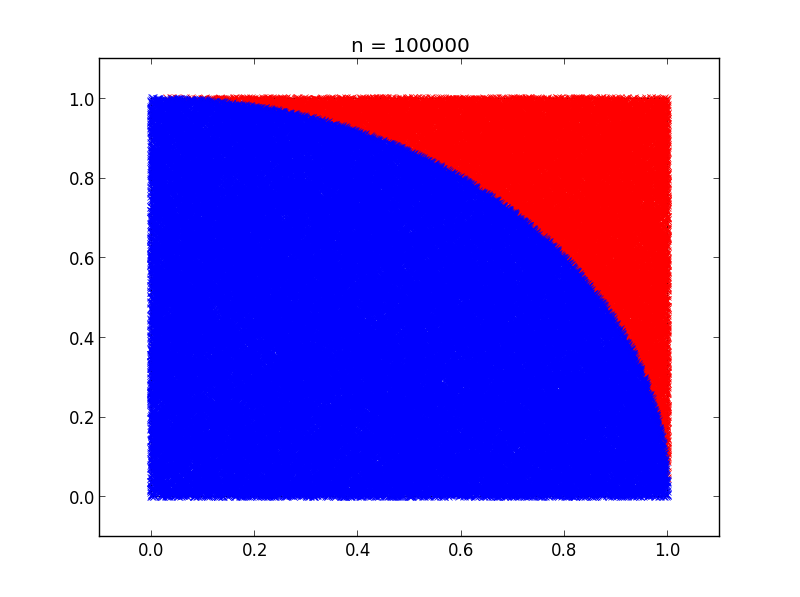
This results in the following estimation of π for each sample size.
| Number of points | Estimation of π |
| 100 | 3.04 |
| 1000 | 3.156 |
| 10000 | 3.1484 |
| 100000 | 3.14052 |
The code for this is very simple, here is a python implementation,
We loop over the total number of points desired (line 7), then generate a random point between 0 and 1 on the x, y plane (lines 8 and 9). Now calculate the distance the randomly positioned point is from (0, 0) if the distance from the center of the circular domain is less than the radius of the circle, then the point is within the circle and a count is incremented. As we are using a unit circle (radius = 1) we can remove the square root when calculating the distance from the center as sqrt(1) = 1
After all of the points are generated, we obtain an estimation of π by multiplying the ratio of points within the circular domain and the total system by four
To finish, here is a canvas implementation of the calculation so that the estimation can be viewed in real time.
| Estimation of π | 0 |
| Error | 0 |
| Points within circle | 0 |
| Total points | 0 |
| Speed |